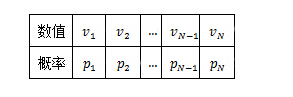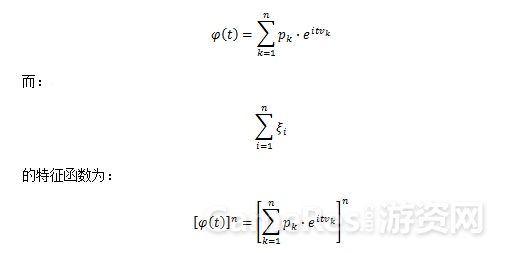在很多回合制游戏的设计中,往往会遇到1v1胜率计算的问题,因为技能等徒增复杂度的不可预测因素的存在,使得理论计算过程变得异常冗繁复杂,而模拟统计方法此时再次凸显其简单易行、安全可靠的优势,被包括笔者在内的游戏设计者们采纳沿用。但后者用高资源(空间、时间)换低精度的效率,不免令人如鲠在喉。
我们知道,模型是对实际对象一定程度的简化。对于这个问题,在剔除一些增加复杂度的“罪魁祸首”,留下单纯的普通攻击之后,加之明晰的战斗规则,1v1胜率的理论计算变得可行。
一、第k次攻击恰好击杀目标的概率
战斗胜利的标志是目标生命值首次被减少至非正数,而此过程又是若干次单次攻击的叠加。
1、必要假设
出于讨论的方便,以及对可能出现的小麻烦的避免,做如下两条设定:
(1)、单次攻击的伤害值ξ(显然ξ≥0)为一随机变量,其概率密度函数为f(x),概率积累函数为F(x),需要指明的是,为了表达方便,这里F(x)的定义为F(x)=P{ξ<x},而不是F(x)=P{ξ≤x}。
(2)、目标有效生命值为H。
2、分析计算
根据上面的假设,现在来计算恰好在第k次将目标击杀的概率P
k。
二、胜率计算
实际上,根据上面的结果:
Pk=Fk-1(H)-Fk (H) k≥1
再结合1v1的相关规则,就可以着手进行战斗双方胜率的计算。为了理解方便,下面将针对一个非常简单的规则进行讨论、计算。
1、具体规则
最简规则:战斗双方从某一方开始轮流交替进行普通攻击,直到其中一方首先死亡为止(对于同时出手的情况,思路和下面将要表述的一致,只不过多一个平手的情况而已,所以这里不去赘述)。很显然在这个规则下,将不会出现平局的情况。
为了表述方便,设定双方的单次攻击伤害值服从同一种分布,且:
2、分析计算
根据上面的规则,不失一般性,假设A先手攻击B。
则A在第k次攻击时胜出的概率为:
三、具体实例
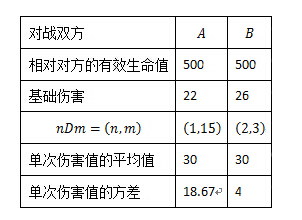
1、假设对战双方的单次攻击伤害的形式都为“基础伤害+nDm(扔n个m面骰子的数字和)”。当然也可以设定其他的分布形式。
从表中可以看出,双方的生命值、单次攻击伤害平均值均相同,但是B的伤害相比较于A更集中一些。我们来看看双方对战时的平均胜率。
2、编程计算
根据前面的分析过程及相关结果,下面给出计算“在A先手攻击B的情况下A胜出的概率”的Matlab函数WinPro:
同样,为了检验理论方法的正确性,模拟统计方法的函数WinPro_Count也是必要的:
将上面的数据代入两个函数分别计算(对于模拟函数,设定次数100万),并给出时耗对比。测试脚本:
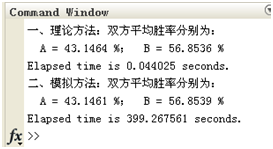
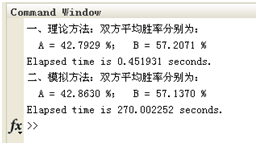
给出结果如下:
3、结果分析
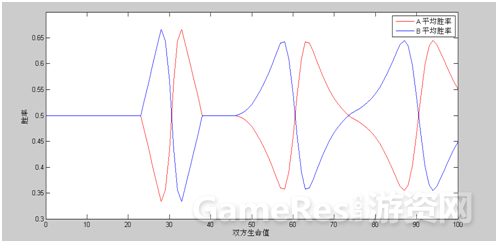
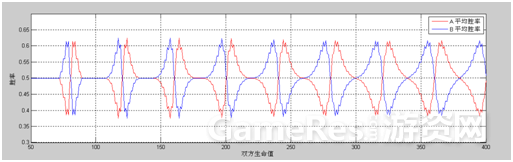
从结果中可以看出,B的平均胜率要明显高于A的平均胜率。为了体现双方胜率关于生命值变化的趋势,笔者好事做计算并出图如下:
(1)双方生命值从0到200的情况(步长为1)。
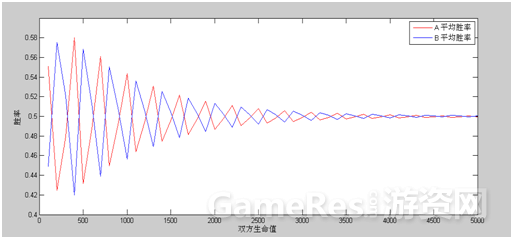
(2)双方生命值从100到5000的情况(步长为100)。
另外,从两种方法的时耗(模拟方法的时耗是理论方法的时耗的9069.1倍)上来看,至少在简化了对战规则的情况下,用理论方法的效率远远高于模拟统计方法。
四、拓展延伸
1、概率分布的统一处理
如果单次攻击伤害值服从更一般的分布,比如连续分布,甚至连续和离散的复合分布等等,对此似乎只能在理论上确认胜率计算的可行性。但如果考虑到以下两个事实:
(1)、连续分布是离散分布的极限;
(2)、实际中(程序层面)对连续情况的实现,从根本上来说用的也是离散方法。
则可以将所有努力倾注到讨论一般化的离散分布上,并且,只要离散程度足够密集,就可以达到对连续分布足够好的描述。
因此,为了描述“单次攻击伤害值ξ的分布”,我们需要将实际分布进行一定程度(取决于N)的离散化,并得到一个对应的分布列:
而多个服从于此离散分布的随机变量ξ_i之和的分布的确定,则可以借助特征函数的方法予以解决。以上面的分布为例,其特征函数为:
再根据特征函数和分布能够相互唯一确定的特性,就可以得到和的分布列,从而为接下来的数值计算铺平了道路。
2、数值计算
根据上面的结论获知,首先需要的是“计算某离散分布叠加若干次所得分布”的函数,笔者将此操作称为“计算分布D的n重离散卷积”。代码如下:
对应得,计算胜率的函数也需要进行必要的修改:
当然还要附带上模拟函数:
以及在给定两组数据条件下的测试对比脚本:
给出结果:
3、结果分析
同样的,将不同生命值对双方胜率的影响规律做成图形如下,以供参考。
从内容上来说,此拓展部分已然将第三部分包含在内。而对于所提供的胜率计算函数,其计算效率是非常可观的,可以拿来作为一般性的工具使用。
五、题外话
1、关于双方的出手节奏
前面的特例中,假设双方轮流交替出手,目的为了进一步简化规则。实际上,对于双方的攻击频率不同的情况,也是可以计算的(即双方的k非同步,或者说步长不同)。但有一个前提,即需要对“双方同时攻击并同时死亡”的情况进行特殊处理(毕竟我们假设没有平局的情况发生),比如设计一个固定的、不同时的、公平的死亡判定方案。
2、关于双方单次攻击伤害值的分布
虽然将一般分布进行离散化后可以比较方便得付诸于数值计算,但是在某些情况下,理论计算还是有一定的必要,而理论方法能否顺利有效(甚至手工计算)进行,在很大程度上依赖于单次攻击伤害值的分布形式。当下的很多设计,有采用均匀分布的,有采用前面例子里的扔骰子的……不一而足。但其特点都是尽可能使分布简单,以易于(程序)实现。
如果撇开实现的难易程度,而只考虑理论上的方便,则应该可以找到一种(或多种)分布,其形式未必简单,但却很容易进行F_k (x)的计算,或者进一步利于后面的相关计算,笔者曾有过这方面的考虑,并初步认为,这种分布至少需要具有可加性(多个同分布随机变量之和的分布函数与单独的分布函数形式统一,满足这一条件的分布是存在的,比如正态分布、伽马分布、负指数分布、二项分布、泊松分布等等),但这还远远不够。如果能够发现所有需要满足的条件,则可以通过某种方法来获得此(类)分布函数,而其中一个具有极高候选价值的方法就是“最大熵方法”。