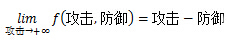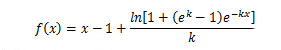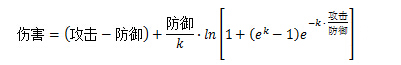对一般化的攻防公式,实际上都可以用如下的形式进行表达:伤害=f(攻击,防御)
而一个理想的减法公式所需要满足的条件:
(1)f(攻击,防御)>0,即没有不破防的情况;
(2)当攻击>防御时:
即此时,攻击-防御是伤害值的主要成分。
如果把防御作为一个参数(用d表示),而攻击作为自变量(用x表示),伤害值为因变量(用y表示)。那么:
y=f(x;d)
进一步,根据d的绝对大小进行单位标准化处理(缩放线性变换),得到:
y=f(x)=f(x;1)
对函数f(x)应满足的条件进行严格的描述如下:
(1)f(x)在定义域[0,+∞)上单调增加,且f(0)=0;
(2)f(x)以直线y=x-1为渐近线;
(3)f(x)尽可能靠近直线y=0和直线y=x-1;
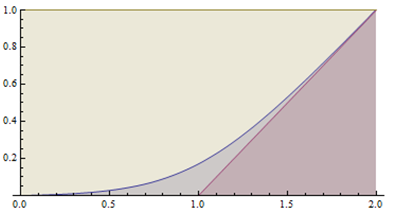
其图形应该如下图的蓝色曲线所示:
考虑两条边界函数组成的分段函数g(x):
| k |
f(1)file:///C:\Users\Administrator\AppData\Roamingencent\QQemp\4D137CC3C5124BCAA4C5522B420A82E1.giffile:///C:\Users\Administrator\AppData\Roamingencent\QQemp\4D137CC3C5124BCAA4C5522B420A82E1.gif
|
1
|
0.212752
|
2
|
0.135300
|
3
|
0.096694
|
4
|
0.074259
|
5
|
0.059913
|
6
|
0.050082
|
7
|
0.042976
|
8
|
0.037620
|
9
|
0.033445
|
10
|
0.030102
|
11
|
0.027366
|
12
|
0.025086
|
13
|
0.023156
|
14
|
0.021502
|
15
|
0.020069
|
16
|
0.018814
|
17
|
0.017708
|
18
|
0.016724
|
19
|
0.015844
|
20
|
0.015051
|
因此,利用如下这个函数:
就可以对减法公式进行改良,结果为:
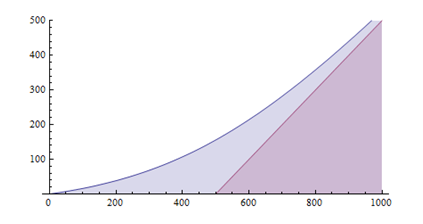
只需增加k值,便可以达到任意的近似程度。图示举例。
(1)、防御=500,k=2:
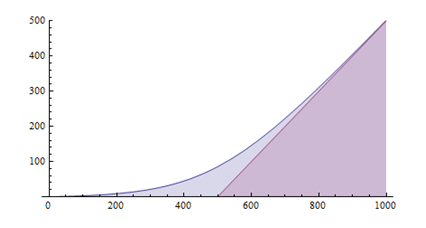
(2)、防御=500,k=4:
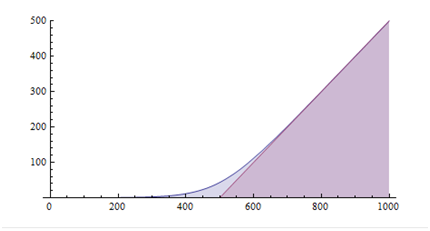
(3)、防御=500,k=8:
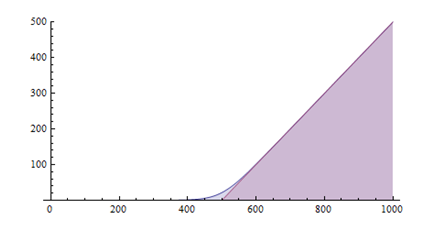
(4)、防御=500,k=16: