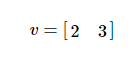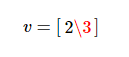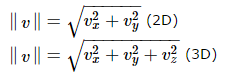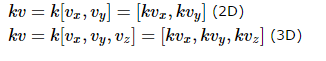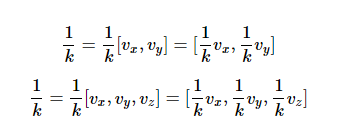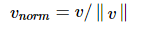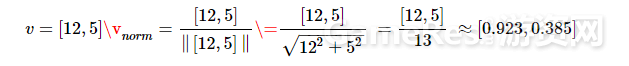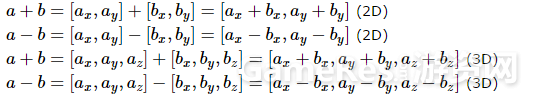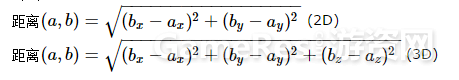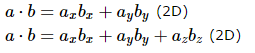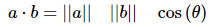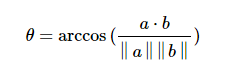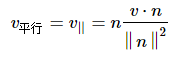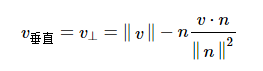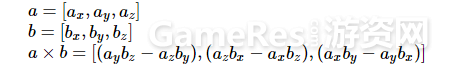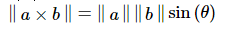图形学与游戏开发：这些公式在游戏开发中很常用

本篇内容来自于书籍《3D图形学基础：图形与游戏开发》，个人总结

1、数学背景与历史

笛卡尔数学由著名的法国哲学家、物理学家、生物学家、数学家"勒奈·笛卡尔"发明。

1.1 1D数学



1.1.1 名词解释

整数：

1，2，3，4，50，-70

自然数：

非负整数，1，2，5，100。

有理数：

一个整数除以另一个整数，可以除尽，结果为，1/2、3/4/、0.88。

无理数：

有些数无法用有理数表示，如圆周长与直径的比值，记作π(pai)。小数点后有无穷的数，除不尽的数。

实数：

有理数 + 无理数的范围，有理数可数，无理数不可数。

离散数学：

研究自然数和整数的领域。

连续数学：

研究实数的领域。

1.2 2D数学


1.2.1 简单介绍

二维可以理解为矩形的网格。

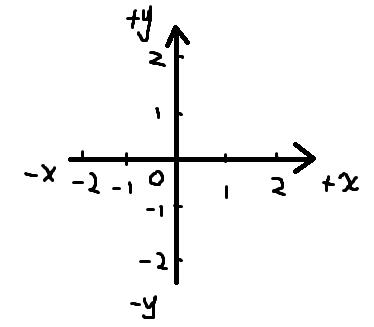
高中时我们用的一般坐标系：横轴左-x，横轴右+x，纵轴上+y，纵轴下-y

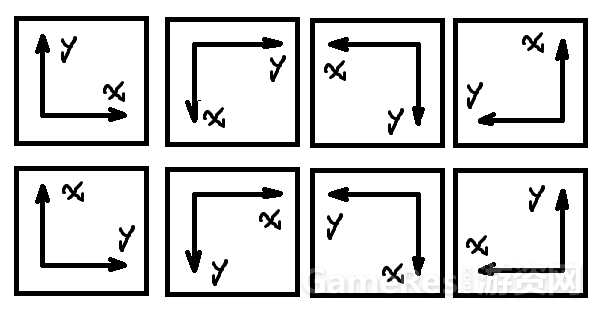
普通的坐标系，通过旋转变换，镜像变换，可以演化出8种坐标系，它们之间都是等价的。


1.3 3D数学：

1.3.1 2种三维坐标系

• 左手坐标系
  

左手坐标系：拇指指向+x，食指指向+y，中指指向+z（远离自己的方向）

• 右手坐标系
  

右手坐标系：拇指指向+x，食指指向+y，中指指向+z（远离自己的方向）

左手坐标系经过旋转变化有24种，右手一样也有24种，总共有48种坐标系

“左手坐标系” 与 “右手坐标系”不是等价的。

下文都用一般的左手坐标系

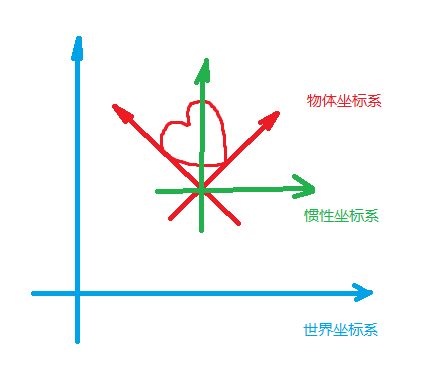
2、多坐标系统

• 世界坐标系
• 物体坐标系
• 惯性坐标系
• 摄像机坐标系
  

3、向量

3.1 简单概念

向量：

“速度”和“位移”是向量，有大小有方向的量叫向量，向量描述位移。

标量：

“速率”和“长度”是标量，没有方向，向量的绝对值，标量描述数量。

3.2 向量的2种写法

一般用小写字母表示一个向量，比如 v。

• 行向量：
  

v=[2,3] (2D)

v=[5,−5,7] (3D)

v=[1,4,8,7] (4D)

可以省略逗号

• 列向量：
  

注意：这2种写法没有优劣之分，一般情况下用“行向量”，因为书写方便

3.3 2D、3D、4D向量下标字母表示

2D:

v=[vx,vy]

3D:

v=[vx,vy,vz]

4D:

v=[vx,vy,vz,vw] (w是分量)

3.4 向量的几何意义

二维向量v=[2,3]可以理解为，在二维坐标系中，从原点开始，先向+x走2步，再向+y走3步到终点，连接原点与终点。

三维向量v=[2,4,5]可以理解为，在三维坐标系中，从原点开始，先向+x走2步，再向+y走4步，再向+z走5步，连接原点与终点。

• 向量相当于表示，位移的序列。
• 向量与点：
  

“点”描述位置，(2,3)是“点”，

“向量”描述位移，[2,3]是“向量”。

4、向量运算

4.1 零向量

可以理解为“没有位移”，标量零表示“没有数量”

4.2 向量变负

几何上可以理解为，向量的方向相反，2D,3D,4D坐标系的操作分别是

−v=−[x,y]=[−x,−y]

−v=−[x,y,z]=[−x,−y,−z]

−v=−[x,y,z,w]=[−x,−y,−z,−w]

4.3 求模运算

求模运算，也就是求向量的大小，向量大小也称为“向量长度”，或“模”。比如有个向量 v，向量标量的绝对值两边加单数线，就是向量长度，记作"∥v∥"

公式：


几何意义：2D的坐标系中，可以用勾股定理解释；3D的证明很复杂，不讨论。

4.4 标量与向量的乘法（除法）：

公式：

乘法


除法


4.5 标准化向量

标准化向量一般用向量名v，加下标norm组成，记作“ ”，这个过程称为“标准化”。
公式：


举个例子：


几何意义：可以从上面的例子中看出，在2D中的标准化后的向量是一个从原点出发，模为1的向量。

4.6 向量加减法

向量a与向量b相加时，可以理解为，A的终点接到B的起点，接着从A的起点指向B的终点就是两向量相加的结果；向量a与向量b在相减时，可以理解为，B的终点指向A的终点的向量就是两向量相减的结果。
（图）

公式：


注意：

向量加法满足交换律，向量减法不满足交换律

永远有a+b=b+a

但a−b=−(b−a)仅当a=b时，a−b=b−a

4.7 两点间距离公式

公式：


4.8 向量点乘

也称作“内积”，结果在几何中表示2个向量的“相似”程度，a点乘b，记作“ a⋅b ”，点不能省略，结果是其夹角的cos值，若结果>0，则夹角0<=θ<90；若结果=0，则夹角θ=90；若结果<0，则夹角θ>90

公式1：


公式2：


有用的推导：用点乘计算2个向量的夹角


4.9 向量投影

求向量vv在向量nn上的投影，能将vv分解为两个分量：v⊥和v||。他们分别垂直于和平行于n，并满足v=v⊥+v||。一般称平行分量v||为v在n上的投影。



4.10 向量叉乘

又称作“叉积”，叉乘的结果是一个向量，该向量垂直于2个叉乘向量组成的平面

公式1：


向量叉乘后向量的长度，为2向量的夹角θsin值与2向量长度的积，这个长度也是a和b向量组成平行四边形的面积

公式2：


叉乘结果向量的方向

在左手坐标系中，若叉乘的两向量收尾相接后是顺时针，则指向你；若叉乘的两向量收尾相接后是逆时针，则远离你；右手坐标系则相反

5、Vector3类型

关于这个类型的实现，每一种语言都有不同的实现方式，从书中看到的结果是，定义了Vector3类有自己的构造方法，并且对常用的运算符进行重载，加了一些常用方法。

我相信，在unity中的Vector3也有相应的操作，比如点乘操作用方法来表现，而不是去重载“*”算符。

这个类基本上游戏引擎都会实现。

相关阅读：图形学和游戏中的虚拟现实编程