游戏数值设定

2016-12-20

Written by Mervin

公式篇

数值设定的步骤很多，本文只讲公式类型、特点及应用；牵涉到数值设定中常遇到的几种类型的设定：几率、经验、属性、技能；本文由简入烦，主体以公式的类型、特色来划分章节，穿插几种类型的设定讲解。

OK，Let’s Begin。

加减乘除

线型为线性，变化稳定，比较容易找到规律，预期后面的发展；

举几个例子：

每加一点力量，近战物理攻击加1；每射击一次，子弹数减少1；

每使用一次冰箭术，熟练度加1，达到2000时，升级为2级；

宠物近战物理伤害=宠物物理攻击-目标物理防御；宠物近战物理伤害=宠物物理攻击*目标物理吸收比；近战物理技能伤害=（（武器伤害+技能附加）*技能增幅）*目标物理吸收；

血击（技能）：在HP <50%时，将自己所有HP化为伤害，攻击目标，使用后生命值为1；伤害=（基本伤害+当前HP）*(1+技能等级调整值+10*当前HP/最大HP)；

总结：

加减的运算最为直观，一眼就可以发现规律，甚至潜意识；乘除的运算容易简单、直接的对数据造成跳跃性，而常常是有意识、有规律的跳动；混合运用时，可以实现很多有特色的功能；

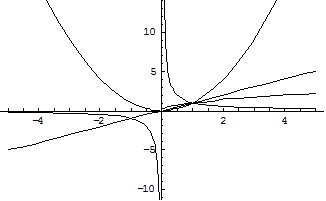
幂函数

幂函数f(x)=x^i；对比函数g(x)=x；


当0<i<1时，[0,1]区间内，f(x)>g(x)；[1,∞]区间内，f(x)<g(x)；先急后缓；

当i>1时，[0,1]区间内，f(x)<g(x)；[1,∞]区间内，f(x)>g(x)；先缓后急；

当i<0时，[0,1]区间内，f(x)逼近无穷大；[1,∞]区间内，f(x)逼近无穷小；


示例曲线图如下：



























于是，这个问题转化成：将s-x个球放入x个口袋中，每个口袋最多能装y-1个球，有多少种分法？

举几个例子：

某盗贼的闪躲为20%；即Random[integer,{1,100}]≤20时，闪躲成功，否则失败；

某盗贼的闪躲为20%，格挡为10%，两者优先级等同；即 Random[integer,{1,100}]≤20时，闪躲成功，21≤Random[integer,{1,100}]≤30时格挡成功；

某盗贼的闪躲是20%，格挡是10%，完全闪躲是25%，优先级完全闪躲>闪躲=格挡；即Random[integer,{1,100}]≤25时，完全闪躲，否则，Random[integer,{1,100}]≤20闪躲，21≤Random[integer,{1,100}]≤30格挡；

弓的攻击是2-10，弩的攻击5-7；便是2dy1和5dy2（y1>y2）的简化应用；（当然，实际效果是1d9+1和1d3+4）；

总结：

我将例1、2中的随机数称为部分随机数，因为存在部分的无用数；

骰子是随机数的一种特殊情况，总是有解，我称之为完全随机数；
几率都可以用p(x,y,s)表达；

p(x,y,s)中的x控制曲线的坡度，y控制曲线的左右跨度，s决定几率大小，x*y决定曲线的成长性；x:y决定曲线的整体走势；

接上，当1←x<y时，趋于平缓；y<x→xy时，趋于陡峭；

任意一种随机数的随机事件都受到收益递减的影响，见下图，表示的是在闪躲提高时，闪躲成功：不闪躲的比例：



p(3,y,s)在s∈[3,y+3-1]上递归增长(一元递归)，规律如下（x=3）：

1,x,2x,3x+1,4x+2,…,ix+(i-2)，…，

或者表达为（将上式看做一个数列）

{p2-p1,p3-p2,…,pi-p(i-1),…}为等差数列，首项p1=2,等差d=1；

p(4,y,s)有类似规律，为二元递归；

若y1<y2，p1(3,y1,s)在s∈[3,y1+3-1]和p2(3,y2,s)在s∈[3,y2+3-1]，p1和p2在s∈[3,y1+3-1]上相等；

[3,y+3-1]区间存在一个递归减少的对称区间，对称轴s=(xy+x)/2；

作者的话

对于数值设定是一项庞大的过程，需要很清晰的思路和逻辑，工作流程不多螯述，做过的基本都知道；不想对哪部分重要、哪部分次要做评价，个人觉得这是混泥土和钢筋的关系，一个发挥不了作用，结合才是正道。
作者的信条是：条件决定结果，尽量简化过程，懂的取舍，懂的轻重；

本篇是第一弹，正在努力推出其他部分的一些东西；因为公式的内容相对比较具体，有很多前人的经验在铺路（虽然正态分布部分的内容完全是自己总结出来的，汗啊，高数学的差的结果，觉得有这么个东西，但就是想不起来）。

特别申明一下，正态分布部分的内容因为没有太多实际的操作经验，所以不太好胡乱举例，避免引起误解。

起点篇

本篇是数值设定相关文稿的第2篇，前篇第一篇讲述的是计算公式的特点及应用。在本篇中，你将了解到作者对游戏中的数学建模的方法和理论，以及实际案例。本篇的主要内容为建模的起点和方法问题，并没有详细、深入，这部分的内容将留到后续章节。

以下是正文（以上是废话）。

我认为：

一个模型必然由有限个模块组成，研究模块的特性是建模的起点；

一个模块具有五个特性：生成、成长、消亡、变化和联系；这五个特性或多或少的存在于模块之中，影响着模块的最终形态。

Ø  生成：这是一个开始，模块产生的原因、过程及一个描述。模块的产生并非是YY出来的，势必是符合大前提的。比如我们的世界观定义在了中国北宋年间，那么就不可能存在八旗子弟。过程，讲述了一个模块生成经历。有的时候，我们需要生成的东西已经是人所皆知的了，往往省略了这一部分，比如武侠，但很多时候是我们创造出来的，比如牛头人，我们需要详尽的描述这个生成的过程，他或者是符合逻辑的，或者是符合人类情感的。“描述”指的是所生成的模块具有的特性，所影响的事物等；

Ø  成长：成长是人类的一种基本情感，一成不变的事物很难得到人的认同，而实际上，万事万物也是在成长的（当然，也在消亡，见下）。这是我将其纳入到模块的特性中的原因。这个特性用来描述模块从起始一步一步成长的轨迹，缓慢还是快速，平稳还是跳跃，……

Ø  消亡：包含两层含义，消失和灭亡。消失，是成长的反义词，一个负成长的模块就是在消失，一个成长环境中的不成长模块，也是在消失。而灭亡是消失可能走到的尽头。比如大家都最容易等级的增加，属性的增加就是增长的例子，而就属性的增加而言，并不是所有属性都在增加的。又如某游戏有10个职业，但是80%的玩家都选择了其中3个职业，这就是另外7职业的一种消亡。消亡不一定就是坏事。

Ø  变化：简单的说，就是模块并不总是朝着一个方向成长，而且成长的过程中会受到很多的影响。这个我想大家都很容易理解，求新求变是变革的根本动力，变化才是永恒的生机。

Ø  联系：模块之间的联系，这是模块可以组成模型的最根本因素。建联系就像织网一样，你想网住多少鱼才会用到什么样的网。

以上就是我在建模时考虑到的五个方面。

到这里为止，没有提到“起点”的问题，下面就以几个常用的起点来就五个方面进行实例阐述。

起点1：背景、种族

在很久很久以前，在某某大陆上，种族A和种族B时战时停，时好时坏，几百年的历史中，使得各自的版图基本明确了；但A族的阴谋家X为了得到无上的力量，不惜出卖灵魂来研习黑暗魔法，以获得与异界联系的能力，并与恶魔订立了黑暗协议，只要能让X得到他想要的力量，这个大陆上的一切都可以被恶魔拥有。终于，在牺牲了99999个人的灵魂之后，打开了异界的传送门，恶魔开始了入侵计划；

恶魔派出了几个猛男带领着他们的奴隶——种族C通过传送门进入了这个大陆。种族C被不断的派往前线，鲜血、牺牲、屠杀、暴力充斥着种族C的灵魂，直到有一天，一个被强暴了A族女人生产了一个混血儿——C族的混血。

A族社会被震惊了，所有人都要求烧死这个孩子，因为他的恶魔血液家给A族带来不幸，女人也被所有人唾弃。伟大的母性使得这个母亲带着自己的孩子逃离了家乡，来到了B族的领地，这里的人们对异种族的并不排斥。孩子长大成“人”Y，受到教育，也了解到了自己的由来以及种族之间的关系。一个伟大的领袖产生了……

艰苦卓绝的战斗开始了……（省略N字，需要很细的情节文字）

终于Y带领着脱离恶魔控制的C族和A族、B族共同击退了恶魔，大陆进入了新的篇章……

成长部分结束。

生成部分：

种族A：人类社会，数量众多，形形色色，对外族持有戒心（实际上彼此之间也不是完全信任），君主统治，君主有着生杀大权，贵族对平民的欺诈和压迫，重视血统。身材中等，男性明显强壮于女性。

种族B：杂居人群，严格意义上不能称为一个种族，因为没有明确的血统。主要人群有脱离贵族控制的人类，妖精，混血人群（人妖 ^_^）。社会中小团体现象明显，人们往往只对一个生活圈中的人群表示认可和交往，一旦彼此得到信任，将是至死不愉的友情。没有明显的阶层划分，过着自给自足的生活。

种族C：异界的种族，相貌丑陋，体形魁梧，皮肤深棕色，眼睛天蓝。面部器官较人类更为突出、明显。身高与人类相仿，但体重为1.5到2倍。多为男性。脱离控制后，形成母系社会，女性地位很高。智商较其他种族偏低，因为曾受到恶魔的洗脑。虽然已经脱离了恶魔的控制，但是对种族A和种族B的伤害使得无法得到谅解，被认为是“潜伏的恶魔”，所以居住地远离人类，过着近乎原始的生活。

种族D：神秘的种族，在种族A和种族B的几千年历史中从没有出现过，在恶魔将种族A和种族B逼到无退路的时候，以神一般的形态出现的种族。详情参见背景故事。这是一个生活在地底的种族，普遍身材矮小，只有人类一半大小，但相貌、身材比例颇与人类近似，犹为突出是相貌都很精致，被人类成为“上帝的艺术品”。在战争结束后，人类才慢慢从使节了解到一些种族D的历史……一个高智商的种族，科技发达，魔法发达。

消亡：本部分搀杂在背景故事之中，主要指种族A地位的降低。

变化：最大的变化就是B种族的设定，任何一个种族，都有杂居和群居这2种形态，代表了两种截然不同的世界观和信仰。种族的出现也导致了对种族A和种族B的发展变化，魔法的渗透很快使得2个社会起了翻天覆地的变化。

联系：种族D完全是一个高贵的种族，不仅仅是大陆的救世主，更是力量的源泉（后续情节发散点^_^），A种族和B种族依然在战争，C种族则与世无争，在自家的一亩三分地上辛勤耕耘，但也丝毫容不得他人的进犯。

起点2：职业

这次来个中国特色的。我们要做武侠游戏，要把技能做的到位，技能是一切之本。OK，我们开始。

中国武侠，博大精神。自盘古开天辟地……（省略N字马屁……被打 :-)）

假设（以下都是本人YY）：

功夫分为：内家功夫、外家功夫和暗器功夫；

内家功夫主要锻炼人的意志力、气劲，是一种精神上的修炼。主要表现在比常人需要更少的睡眠、领悟能力、预知能力（但感官迟钝）、以气来杀伤、御敌和调理身体技能；

外加功夫主要锻炼人的身体，是一种身体上修炼。主要表现在比常人更有耐力、身体机能好，不如被疾病缠绕、物理打击能力强、感官敏锐（但不善于预知）、轻功好（虽然内家功夫也有轻功，但原理不同）；

暗器功夫：指使用暗器、毒的功夫。

每个人都或多或少的具备以上3种能力的1种或几种。

生成部分介绍完毕。

变化部分开始：（以外家功夫为例）

外家功夫分为强身和轻身两系；

强身系以增强体制、锻炼臂力为主，达到以掌碎石、体制健壮的目的；

轻身系以锻炼灵巧性、身体协调性为主，达到动作行云流水、制敌于手起手落之际的效果。

强身系更善杀敌和御敌，轻身系更善制敌和自保。

成长部分开始：（以外家功夫——强身系为例）

从“概念”上我们将强身系修炼分为10级。

我们简单的用下面这个表来简单描述一下成长轨迹：

级别	描述
1	马步、打桩等基本功；
2	基础武术修炼（18般武艺）
3	选择分支，选择武艺类型
4	抗打击等中级基本功
5	中级武术修炼
6	选择分支，选择细节武艺类型
7	铁砂掌等高级宜守宜攻的外家修行
8	高级武术修炼
9	最后专精冲刺
10	金刚不坏、融会贯通

*必须注明的是，成长部分很容易嵌入到实际的建模过程中，而且比较细致，属于工作量最大、最复杂的部分。为了不迷失自己的方向，我建议先做好框图表，从概念上将成长“钉死”。