是时候重新审视AB测试了

译/猫猫喵喵

本文转自游戏网站Gamasutra.com的社区博主Viktor Gregor，原文地址在此，一段时间没有更新了，考虑来一个硬一点的菜，就选中了本文。本来我不想翻译与手游有关的内容，但是考虑到游戏运营这部分尽管更多运用于手游，但并不是手游的专利，另一方面也是因为这篇文章的确写的很有水准，并且相信能对最直接的经营思维提供一些有价值的信息。

由于文中涉及到不少有关统计学的知识，作者的主张是贝叶斯方法对游戏版本更新提升氪金能力的影响进行AB测试，大家可以参考查阅相关梳理统计方面的知识。另，由于本人是学渣，统计相关的知识只是以前用SPSS的时候钻研过，并没有非常坚硬且系统性的知识体系，加上是从英文翻译，部分知识点的确超出了我的知识范围，我也是一边查资料一边翻译的，所以如果有什么低级错误希望大家指出，非常感谢！

---

前言

我想在本文中解释一下为什么我们Pixel Federation会决定彻底的改变使用A/B测试的方法，我们会比较对F2P类的手游的不同版本进行AB测试的新旧办法。

我们常常回去测试两个版本的游戏，（通常）版本A是现阶段的游戏版本，而版本B是加入了一些新特性的不同版本——调整了平衡或者其他什么，以前，我们通常使用“虚无假设检验法”进行测试（NHST，null hypothesis significance testing），也就是大家熟知的频率测试（frequentist testing）。具体说，就是我们首先使用卡方检验来测试转化指标，然后对收费指标进行T检验，如ARPU（每用户平均收入）或ARPPU（每位付费用户的平均收入），而现在，我们使用贝叶斯检验。（译者注：卡方检验和T检验都是统计学上的常用工具，简单理解，假设你对游戏中某些细节做了调整，运用卡方检验，可以确定新版本的改动，是否对于转化率变化产生了符合预期的促进作用。T检验是可以分析出，不同版本有没有对于客户付费的心理产生影响（或者说吸引力更多愿意付费的客户）。而贝叶斯检验则（理论上）可以分析出，现在的这一版改动，对于各项指标的改进是否朝着预期的方向前进。）

我介绍一下我们为什么要把测试方法换成贝叶斯检验：

（1）可以解释结果

（2）样本大小和测试设置

1、如何解释结果？

由于频率论和贝叶斯统计对概率和假设检验的处理方法是截然不同的， 因此我们从相同的数据中得出的结论也会大相径庭。

解释频率测试方面

频率测试会得出一个p值以及置信区间，通过将p值与预设的α水平（通常为5％）进行对比，我们可以判断某个结果是否是“显著的”。 这种方法已经用了100多年了，并且没什么问题。 但是求p值这个部分却存在一个大问题，很多人以为自己理解了它，其实大部分是没有的。 这就可能导致许多问题，比如无意是下的“p值黑客”（P-hacking）问题。（译者注：p值黑客简单的理解就是“应试教育”，一旦考试中规定了某个指标作为唯一的判别标准，就会诱导人有意无意的去仅仅只追求那个指标，例如其实啥知识都没学到的“考试型选手”，以p值为唯一的判断标准，就会诱发这个问题，我们把这种情况称之为“p值黑客”。）

主要是因为p值并非一种直观的指标——如果我们想测试A和B之间是否存在差异，我们就必须先形成设定一个“虚无假设”，就是假设一个“否定的结论”（例如A等于B），然后，我们收集数据并观察他们，看他们与这个结论相比起来差异大不大，之后，我们才能从p值的结果中得出所观察数据的概率与（之前所做的）虚无假设相差甚远（然后反推出所观察的数据与我们预设的数据之间没有差异）。（译者注：这里有点拗口，简单理解就是，p值假设来验证一件事情的方式，并不是用“这件事真不真”这种直观的表达，而是采用类似“这件事如果反过来说，这个反过来说的结论是否并不真实”这种多层否定的逻辑，如果不是用习惯了的话，非常容易把自己绕进去，而且当把这个结果带入到更复杂的一套逻辑中后，就会导致那一整套逻辑特细变得特别复杂，难以方便的思考。）

换句话说，如果我们进行AB测试（注：原文这里写作“A/A test”，联系前后文应该是笔误），p值告诉我们的是，我们所获得的结果概率与实际观察到的结果是一样极端（或更极端）——这已经是我所知道的最简单的p值描述了，但它似乎仍然让人难以理解。

我并不是说复杂的事情就没用，但在我们是需要在商业层面上让我们的业务人员和游戏设计师们能理解我们的结果的。

那我们该如何解释我们的这些结果呢？如果我们得到p值小于alpha的结果，这就表明一切都很好。我们得出了A和B有所不同的结论，明确了商业上存在价值了，之后每个人都会因此很高兴我们做了一个成功的A / B测试，不过，却没人关心他们并不明白的p值究竟意味着什么。

但如果我们没那么幸运呢？当我们得到高于alpha的p值时，实际上是很难得出具有一定价值的结论的。我们可以看一下下面的例子：这是一次卡方检验的结果（由Evan的Awesome A/B Tools计算得出）。


我们不仅无法得出结论认为哪个版本更好，也无法认为（新版本）没产生变化。现在，我们唯一知道的就是p值等于7.2％这个结论。我们也有置信区间，但在这里没什么用，因为所存在差异的置信区间包括0。（注：理解这里需要一点数学基础，简单理解就是，差异的置信区间如果包括0的话，可以认为“前面的这个p值的可信度是有问题的”）。现在，生产团队的人很可能无法理解等于7.2％的p值是什么意思，如果你试图用某种方法向他们解释，那可能会让情况更糟。 因为我们假设了一个我们不希望发生的结论，那谁会愿意去关心“我们得到的结果比我们假设的前提更极端”这件事？

在这种情况下，你（反而）可能很容易会说“嗯，7％非常接近5％，看起来有效果。那应该就是B版本更好啦”。但实际上你是不能这么做的，因为（理论上来说）如果没有实际效果，p值就会均匀分布在0和1之间，也就是说，如果A和B之间确实没有差异，那p值等于7％或者等于80％或任何其他数字的概率是相等的（译者注：也就是说是均匀的分布在整个概率区间上，如果有所确定，那么就会集中分布于某些概率区间上，举个例子，你如果没有证据表明明天你会不会被天上掉下来的石头砸到，理论上就是不会砸到50%，会砸到50%，概率“均匀”的分不到“砸到”和“不会砸到”两个结果上）。因此，你能维护身为一个统计学家的正直性的，就是声明：在当前的测试中，当前没有足够的数据支撑任何判断。

这让人非常沮丧，因为A B测试是非常破费的。从管理者的角度来看，我们进行几周的测试，然后分析师也得出了结论，但是我们看起来基本上都没意识这样做是在浪费时间和金钱。我看到大家很失望，导致以后也不愿意进行AB测试了，这不是我想要的。

解释贝叶斯检验

贝叶斯方法很好地解决了上述问题，因为它可以在任何情况下都能为我们提供有意义且易于理解的信息，他在使用过程中不需要进行虚无假设，这就使得他在解释的过程中简单了许多。

贝叶斯检验的结果不是p值，而是下列三个数字：

•P（B> A） - 版本B优于A的概率

•E（loss| B） - 如果B版本有问题，那问题又多大

•E（uplift | B） - 如果B 版本很好，那究竟有多好

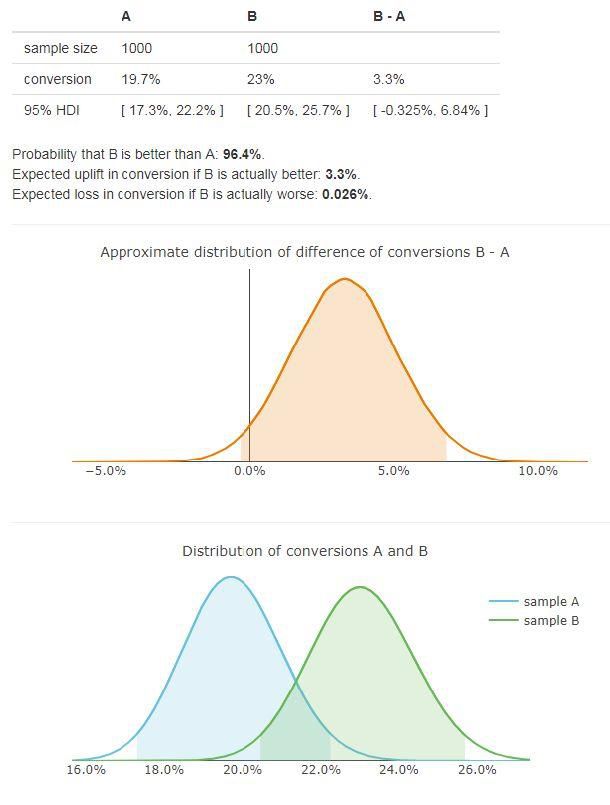
而且E（loss| B）和E（uplift | B）两个结果在测试过程中所用的单位是一致的。 如果是转换，如果（二者）需要换算对比，（结果）就是一个百分比，接下来让我们看一下，之前的数据（在这种方法下）产生的结果。


结果告诉我们，如果我们选择版本B，结果（一方面）可能会变得更糟（概率为3.6％），我们可以预测会产生0.026％的转化率损失。另一方面，我们的选择更可能是正确的（概率为96.4％），我们预期能在原本23％的转换率基础上有3.3%的提升。这是一个简单的结论，游戏设计师和管理者们都能很好地理解。

要确定使用版本A还是版本B，我们就需要在测试结果得出前先确定测试的规则。你可以根据P（B> A）来决定，但如果你仅仅只需要确定E（loss| B）的结果小于某个预定义的阈值，就可以宣布B是更好的选择，这种方法就无疑是更加明智的。

虽然这样的决策机制并不如p值那么明确，但我认为这是一件好事。 “p值<5％”在每个统计学家脑海中都是一个让人紧张的东西，因为我们甚至常常难以确认这个结论在当下背景下是否具有意义。而在贝叶斯测试中，我们需要在测试之前就与游戏设计师讨论E（loss| B）的阈值，然后我们就可以将阈值设定为一个非常低的数字，低到我们不用去关心是否会出现（比阈值）更低的误差错误出现。

但即使预先设定的决策规则无法在不同变量中区分出差别（例如我们没有足够的数据，或者我们将阈值设置得太低），但至少我们也还可以从对比在P(B > A)的概率下的预期收益及在1 – P(B > A)概率下的预期损失之后，做出一个明智的判断。这就是贝叶斯测试在具体应用层面上最主要的优势所在，总而言之，就是你总是能从中获得好理解且有意义的信息。

2.样本规模和测试设置

到目前为止，我只提到了有关如何理解测试结果的问题。使用贝叶斯测试还有另一个关于样本量的非常实际的原因。NHST最常提到的缺点就是需要在测试开始之前确定样本规模的大小，而贝叶斯测试没有这个要求，除此之外，它通常在样本规模较小的测试中表现会更好。

频率测试中的样本规模

在NHST中需要确定样本规模的原因在于我们如何去收集数据将会影响到p值，例如当我们设置的测试目标分别是来自10000名玩家的观测（数据）与来自100名玩家的观测（数据）时，我们就应该（用）不一样的（方法）去计算P值。这听起来有点违反直觉，而且常常被被忽视，这是由于，一方面是人们会认为（分析）数据本身就是足够的，但是如果你想计算出正确的p值，你就不能如此。我不打算在这里解释它了，因为John K. Kruschke在其论文中（见图10）已经进行了很好的分析，他在他自己的书《贝叶斯数据分析》（<Doing Bayesian Data Analysis>）中第11章里进行了更详细的解释。确定样本大小的另一个原因是我们需要对统计测试的效力进行一些估计。

这意味着我们必须在收集数据之前确定测试中会包含多少玩家，然后仅在达到预期的样本规模后才能评估结果。但由于我们通常不知道效果的实际大小，因此很难正确且有效地设置测试。由于AB测试很昂贵，所以我们会希望尽可能高效地安排测试。Evan Miller在一篇文章中详细介绍了这个课题。他清楚地展示了“窥探”（译者注：对一个时间点上的数据进行切片分析定性，我们可以称之为data peek，也就是数据窥探）是如何在达到预设的固定样本量之前，引发测试结果中的第一类错误的比例大大的增加，导致结果变得完全无效的。

（译者注：第一类错误是一个统计学概念，又称Ⅰ型错误、拒真错误，是指拒绝了实际上成立的、正确的假设，简单理解就是第一类错误：原假设是正确的，却拒绝了原假设。也就是说我们如果预设P值，简单理解就是我们预设了一个“我们容忍5%概率以下犯第一类错误的概率，认定目前的结论”）

他还提出了两种可能的方法来解决这个“窥探问题”：序贯检验或贝叶斯检验。

（译者注：peeking problem，也就是peek引发的问题，假设我们基于一个p值下进行一次peek，理论上我们所接受的内容中是存在5%的第一类错误的，基于接受上一次peek 的结论而进行的下一步假设检验就会把数据中携带的5%的第一类错误“遗传”下去，如果测试不断延续下去，就会造成第一类错误的“堆积”，另，序贯检验是一种测试之前不确定样本量规模，而在测试过程中确定样本量规模的假设检验方法）

贝叶斯测试中的样本规模

贝叶斯测试并不需要锁定样本规模才能提供有效结果。你甚至可以反复测试结果（这一点几乎被认为是对NHST测试方法的侮辱），并且结果仍然有效。但是我必须给大家一个大大的警告！一些文章声称贝叶斯方法“对于Peek免疫”。这种表述可能会产生误导，因为这种表述会让我们以为，即便我们有条不紊的检查结果并在出现显著结果时停止检测，第一类错误率可以保持（在可接受范围）。其实并不是这样，目前在统计学里面，如果你有一个基于某些极值的观测的测试停止机制（比如P<0.05），那你就不可能做到（维持第一类错误率在范围内），事实上，贝叶斯检测从一开始就没有一个约束性的第一类错误率，它是一种不一样的方法，但它却存在一个作为约束的预期损失率。David Robinson在这篇文章中表明，贝叶斯检测的预期损失在“窥探”（Peeking）的时候也是收到约束的。所以，这种观点部分是对的，但是需要意识到所谓的“对窥探免疫”对于NHST方法来说意味什么，在贝叶斯检测中则是指别的东西（译者注：贝叶斯测试不是对于peek免疫了，而是因为其问题不在第一类错误率上，而在预期损失率上，所以等于说贝叶斯方法是“避开”了第一类错误率，而不是消除了它）。

如果你需要特别关心第一类错误率方面的问题，那我需要警告你，在这类情况中，贝叶斯测试可能并不适宜。

但我总归认为第一类错误率在我们的背景下并不是非常重要，尽管它很显然在医学等科学研究中非常重要，但AB测试是不一样的，因为我们最后总是要选择出A或者B的，如果确实没有差异或者差异非常小的话，我们就并不需要关心我们是否犯了第一类错误，我们只关心所犯的错误是不是很大。基于此，在AB测试上，以预期损失作为约束条件而不是第一类类错误率将更有意义。

除此之外，贝叶斯测试还有另一个实际优势，与NHST相比，它通常只需要很小的样本规模就能实现相同的效力，这可以为我们节省很多钱，因此我们可以更快的做出决策。

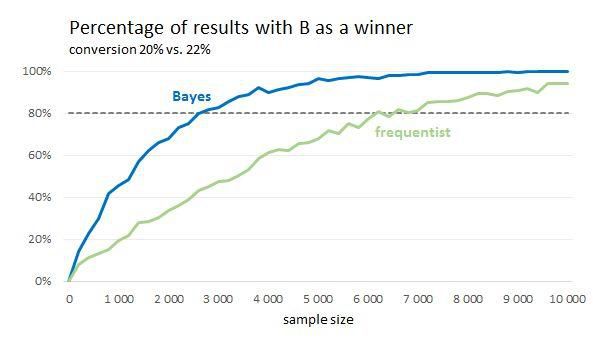
下图展示了对于转化率检测的模拟，我们进行了1000样本量的卡方检验以及1000样本量的贝叶斯检验，并测算出了两个实验中“B为最优解”的分别的预测概率，表现出了（两种测试）在特定样本规模基础上展现出的近似的效力。

我们可以看到，贝叶斯测试在获得80％测试效果上所需的样本规模是显着较低的，不到（NHST的）一半。另一方面，如果我们绘制出A和B两种条件下达到相同转化率时的图形，则（会发现）NHST具有更好的结果（对于样本规模下测试效力均为95％）。

对于卡方检验，我们使用等于5％的alpha值（第一类错误率），当（我们需要设置）预期损失低于0.1％时，（则可以用）贝叶斯测试得出B为更优。


如何在实践中运用

在说完改变的原因后，我还想聊聊我们如何在实践中使用它。目前，我们正在使用两个独立的贝叶斯模型进行两种不同类型的测试，这里就不做详细的解释了（需要单独的文章），我只列出我们目前正在运用的部分。

我们使用的模型不是卡方检验，而是假定转换率具有伯努利分布。所有公式均来自下列来源：

Evan Miller的贝叶斯AB测试公式（Formulas for Bayesian A/B Testing）

Chris Stucchio在贝叶斯AB测试中简便评估决策规则（Easy Evaluation of Decision Rules in Bayesian A/B testing）

对于收入数据，我们一个转化率模型的扩展（模型），它使用指数分布单独估算转换率与伯努利分布，然后估算出支付金额。我是根据这篇论文实现的：

Chris Stucchio的VWO贝叶斯AB测试（Bayesian A/B Testing at VWO）

Kruschke的书中提供的代码对于理解贝叶斯统计数据也非常有用。 我用其中的一部分来计算最高密度区间（译者注：最高密度区间是一个统计学定义，其中密度是指密度分布，密度分布等于一段区间的概率除以该段区间的长度，这段区间也就是事件的取值范围）：

执行贝叶斯数据分析程序

使用这些来源，我在R中实现了AB测试计算器（译者注：R是一种用于统计分析、绘图的语言和操作环境）。你可以在这里尝试一下：

转化率的贝叶斯AB测试

ARPU的贝叶斯AB测试

总结

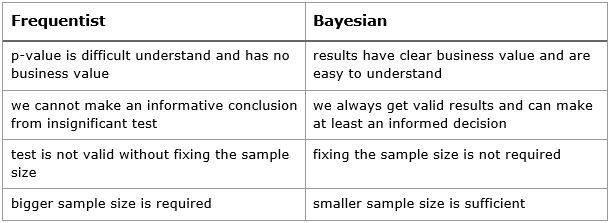
使用贝叶斯AB测试，现在我们可以更快地执行测试，并获得更多可操作的结果。让我一起总结一下，它的优点如下：


那么这种方法还有什么缺点呢？为什么我们不经常使用呢？在我看来，主要原因是与传统的NHST测试相比，这种测试方法实现起来要复杂许多，传统的NHST测试可以只使用Excel中的一个函数就能计算。另外，有些人对使用贝叶斯方法犹豫不决的原因是先验分布（译者注：先验分布，又译为“验前分布”或“事前分布”。是概率分布的一种。与“后验分布”相对。与试验结果无关，或与随机抽样无关，反映在进行统计试验之前根据其他有关参数口的知识而得到的分布，可以简单理解为类似上天偶然给的一个事先的分布）。先验和后验分布是贝叶斯统计的关键要素，在进行任何计算之前，你必须确定这个先验分布。在Pixel Federation，我们目前是将无信息先验用在AB测试上（译者注：无信息先验指的是在没有任务信息的情况下，认为各个点的概率或概率密度相等是合理的，我们没有理由让任意一点的概率大于其它点的概率。无信息先验试图给出一个对后验概率影响尽可能少的分布，一切让数据说话）。

总之，我想强调一点，我并不是说频率统计都不如贝叶斯方法。对于不同的目标它们都是有用的。在本文中，我想表达的是贝叶斯方法更适合商业应用程序。

如果您碰巧遇到类似问题并以不同方式解决了问题，或者您使用贝叶斯统计数据并拥有一些你想分享的经验，请告诉我们。

参考资料：

Bayesian estimation supersedes the t test
Doing Bayesian Data Analysis, A Tutorial with R, JAGS and Stan
How Not To Run an A/B Test
Is Bayesian A/B Testing Immune to Peeking? Not Exactly
Bayesian A/B Testing at VWO
Formulas for Bayesian A/B Testing
Easy Evaluation of Decision Rules in Bayesian A/B testing

来源：奶牛关
地址：https://cowlevel.net/article/2007883