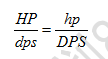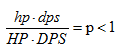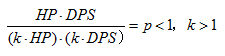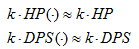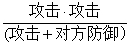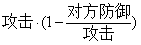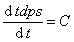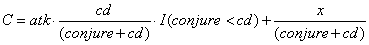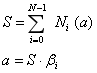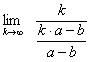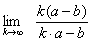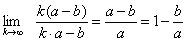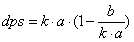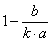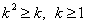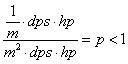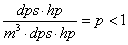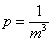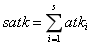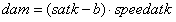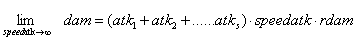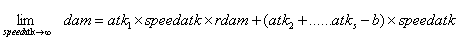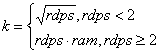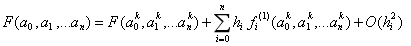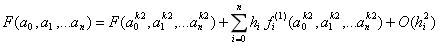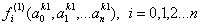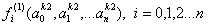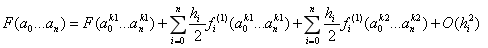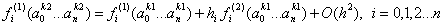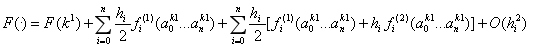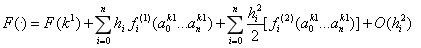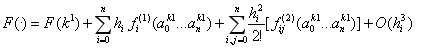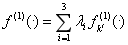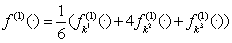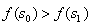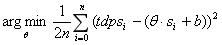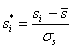游戏数学建模工程手册

2020-05-18

本手册有一个雄心勃勃的目标：将游戏数学建模的工作变得专业、规范和标准，同时像其他工程行业的手册一样，可供相关人士翻阅、应用或得到启发。如果目标能够达成，好处是显而易见的：

1】标准化有利于游戏数学建模的规范、可靠、高效，以及人员的甄别
2】专业性的提高，不仅降低项目开发尤其是数值调试阶段的成本，往往也伴随着收入水平的提高
3】直接或间接的令游戏数学建模发展、发现新的方法，进一步促使其专业化

为达成上述目标，本手册采取了尽可能数学的阐述方式，这种阐述方式具有工程的可操作性，并且避免了不必要和非专业的争论。

手册由如下内容组成：

【评估建模】如同各数学应用领域存在对算法的稳健、无偏、精度、稳定性、一致等指标以评价算法，这部分讨论了什么才是好的模型，又如何评估，它包括：

——时间复杂度
——可操作性
——充分近似

【不好的建模】这部分内容讨论了一些建模方式，这些方式或时间复杂度过高，或缺乏理论联系实际，甚或基于错误的理解，它包括：

——随意添加、滥用参数和运算法则
——滥用战力、价值
——反推数值
——技能循环

【有用的建模】这部分内容体现“手册”一词的含义，讨论了一些游戏实际模型的构建与算法：

——减法伤害公式的近似与应用
——战力的认识与计算
——技能建模：三种算法的综合
——自由分配属性点：最值问题
——经济建模：齐次方程组与样条插值解
——广义PVE模型

【数学建模与游戏开发】作为本手册的最后一节，这部分讨论了游戏数学建模工作者在游戏开发中的作用与位置。









【时间复杂度】时间复杂度是用数学形式来表达、对比同一功能但不同代码之间的程序运行时间，用以横向评估程序的质量。该方法同样可以评估广泛使用excel的游戏数学建模工作的质量。

我们将非重复的写入、修改1个单元格的操作时间花费视为常数1，非重复是说通过如复制、依序拉出、excel函数结果可变的操作仍视为常数1。

先从一个简单的例子开始。属性/道具有两种分配方法，一种是给出总的量分给各系统模块（下称总-分），另一种是系统模块单独给定然后汇总（下称分-总）。那么，这两种建模方法，哪种更好呢？

使用总-分方法时，给出总量所需操作时间为常数1，总计有n个系统模块进行分配各操作1次，累积操作时间为n*1，每个系统模块需要改名来让函数从总量里提取到正确的分配额度同样花费n*1，总-分方法时间复杂度为T(n)=1+2n。使用分-总方法时，除了有总-分方法的操作步骤外，还需在汇总函数里加入n个系统模块的单元格链接来花费n*1，于是分-总的时间复杂度为1+3n。两者在渐近时间复杂度上是一个量级的O(n)，因此n足够大时，两者时间复杂度相差无几，但在实际工作中n不会太大，于是，总-分的时间复杂度更低、更可取。

再以养成模块进度规划（下称游戏节奏）的3种建模方法进一步阐述时间复杂度在建模/模型评估上的应用：根据产耗计算养成模块进度、齐次方程组解析解、齐次方程组插值解。

根据产耗计算养成模块进度——当我们为一个系统模块给定产出和消耗后，这个系统模块的游戏节奏就被确定了，我们需要知道这个游戏节奏情况如何，好知晓游戏内容被玩家消耗的情况、怪物们应该匹配的强度。我们有n个系统模块产出需要规划，其时间复杂度为k*n*m，其中k表示平均而言1个系统模块的时间花费常数，m为道具种类，相应的，我们有m个道具消耗要规划，其时间复杂度为k*m，我们需要计算出生命周期为t的游戏节奏，并且要先汇总产出，则花费t*n*m，于是“根据产耗计算养成模块进度”这种经济建模方式的时间复杂度为T(n)=k*n*m+k*m+t*n*m。1个道具至少安排1个系统模块负责产出，故n>=m，我们取最小值n=m，则T(n)=k*n^2+k*n+t*n^2，其渐近时间复杂度为O(n^2)，随着道具种类和系统模块的增多，这种建模方式耗费的时间以平方级别增长。

齐次方程组解析解——1个方程组代表了1个系统模块的游戏节奏，产出消耗均由齐次方程组的解提供。因此我们需要先规定生命周期为t的游戏节奏，有n个系统模块要规定，其复杂度为t*n，然后设定齐次方程组的系数a_00.........a_tm*2，m*2里的2分别代表产出和消耗，系数用来表达方程组里的本行方程（节奏）的产耗是第一个方程（节奏）产耗的多少倍，花费时间为2*t*n*m。最后，齐次方程组的解析解是基础解系，我们还需线性放大缩小来匹配特定道具数量所需的量级，我们要放缩m个道具的产耗，该操作时间复杂度为m，于是，“齐次方程组解析解”的时间复杂度为T(n)=t*n+2*t*n*m+m，取n=m，则T(n)=t*n+2*t*n^2+n，渐近时间复杂度为O(n^2)，该建模方式耗费的时间仍以平方级别增长，但比起“根据产耗计算养成模块进度”它只有1个高阶项。

齐次方程组插值解——每个系统模块的全部进度必须完整的由齐次方程组表示，插值解方法将其改进为：在一些我们关注的时间节点才规定具体进度，其余节点由插值解自动估计。这样的改进要求我们必须规划产出，用插值求解消耗从而匹配所需的游戏节奏，则规划产出的时间复杂度为k*n*m。关注的时间节点远小于t，因此规定游戏节奏的复杂度仅为n，我们还要汇总m个道具，复杂度为m，则“齐次方程组插值解”的时间复杂度为T(n)=k*n*m+n+m，取n=m，则T(n)=k*n^2+2n，渐近时间复杂度仍为O(n^2)，比起“齐次方程组解析解”少1个线性项，并且没有t。当t较大时，“齐次方程组解析解”用方程组去描述游戏节奏耗时以线性方式积累，当t较小时，“齐次方程组解析解”仍要放缩m个道具。因此，改进方法减轻了时间复杂度里一次项的影响，相对高效。

我们最后讨论一种建模方式的时间复杂度来结束本节。同一用途的道具存在内部品质/级别区别，是不同养成阶段所需。一种方式是将其视为不同道具，然后分布在产出规则细节中（下称细分道具），另一种方式是将所有高级品质/级别的道具视为最低品质/级别道具的特例，与最低品质道具是一个常数k_1......k_n线性放大的关系，其中n表示品质/级别的数量，然后将最低品质道具分布在产出规则细节中，当从某个节点要求特定品质道具时，则将该道具除以k求出高级品质道具（下称广义道具）。

细分道具——我们有n个同一用途不同品质的道具要投放在a个节点上，a起到隔板作用，故a=n-1，复杂度为n-1。平均而言每个节点之间有m个投放点（比如关卡数），需操作n*m的时间复杂度，显然n<=n*m且有n<=n^2，取n=m。于是“细分道具”的时间复杂度T(n)=n-1+n^2。渐近时间复杂度为O(n^2)。

广义道具——在这种方式下，我们仅需投放1个道具并依序给到全部投放点，花费时间为常数1，设置a个节点复杂度为n-1，我们使用以lookup为核心的函数来令所有投放点知晓自己是否应当除以常数k_1......k_n，函数时间花费常数1，要设置n个常数k复杂度为n-1（因为k_1始终为1无需设置）。举例来说第1个节点填写k_2，由于k_n>k_n-1....>k_1，因此lookup固定头部单元格后道具只能查找到最后的非空值k来除以它。于是，“广义道具”的时间复杂度仅为T(n)=n-1+1+1+n-1=2n，渐近时间复杂度为O(n)，时间复杂度为线性的“广义道具”方法优势明显。

不同于程序输入不同规模的数据实际的查看算法的运行时间来精确比对，游戏数学建模只能使用T(n)和渐近量级的O(n)来讨论。时间复杂度是一个衡量、评估数值策划建模效率的工具，如果太多建模部分的方法时间复杂度较高，尤其是多项式或指数级的（以及模型面对的目标庞大的），那么整体的时间花费同样较高，这也是多数数值策划工作的现状。

可操作性

——伽利略

【可操作性】和常识用语甚至哲学讨论不同，所有工程应用均强调可操作性，并且以如何操作的描述来确立名词，称呼为操作性定义。同为工程应用数学的游戏数学建模，也应遵循这一原则：充分描述建模的操作过程、细节使得他人可以复现。

用一个简单的例子来引出我们将讨论的可操作性：饥饿这一说法不具备可操作性，我们使用未进食t小时来描述它。这个例子包含了如何测量以及量化的单位，接下来让我们看看更多的例子。

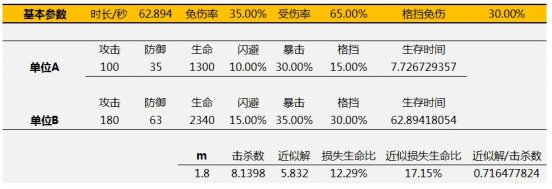
战斗平衡是一个经常会提及的词汇并且我们需要为之建模，大体上我们对它的理解并不含糊，尽管有时会被滥用在与其含义擦边的地方。我们将战斗平衡描述为：在有限的时间t内，2个战斗单位均以100%生命值为代价击败对方。它如何具备可操作性？已知描述2个单位战斗过程的基本公式：



将所有参数移到左边：



作为工程应用数学，右边的1我们赋予其现实意义：100%生命值（在后文我们还会看到它有另一现实意义）。根据这个公式，2单位的战斗平衡意味着调整左边任意参数的线性放缩，使得等式恒为1。在得知平衡的操作方法后，自然延伸出战斗优势的可操作性：1个单位仅需p且0<=p<1的生命比例为代价，我们称这个单位有1-p的优势。战斗优势有一个不够中立的称呼“不平衡”，然而不平衡也意味着角色通过成长、付费等途径获得好处，所以本手册以中立的战斗优势来称呼这种情况。

另一个可自然延伸出的是战斗体验的可操作性。显而易见，战斗体验由诸多因素组成，许多因素难以操作和量化，如果我们苛求这些并一头扎进繁杂的细节里，除了得到一堆猜想外只会无从下手。任何模型都是对现实的简化和比喻，我们对战斗体验的建模用2个指标来逼近这一现实：在一个有限的时间t内损失生命比例p。t和p都小，量化了一场简单/新手的战斗。t小p大，量化了一场容错率低的战斗，从而很适合玩家体现自身操作水平。t大p小量化了一场检验玩家输出是否达标的战斗，超时后怪物将秒杀玩家或根据输出决定奖励分配。t和p都大则是一场充满史诗感的对决。

既然付费是获得战斗优势的一种途径，那么我们当然可以将付费体验可操作化，给定付费额度可额外获得多少属性，使得：



分子位置为非付费玩家，分母位置为付费玩家。当付费额度是一个常数时，p越小，战斗优势越明显，付费体验便越好。

以上例子表明，可操作性要求我们给出建模达成的量化方式、如何达成这个结果以及最后但并非最不重要的：结果是工程应用性质的。工程应用性质意味着建模结果是玩家容易感知、理解的（如上述的生命比例）。接下来提及的2个例子进一步阐述“工程应用性质”的含义。

有一种经济上收益相关的建模方法，即在养成模块的某个阶段发生突变，比如给的属性更多但所需消耗更少从而改变玩家的收益感，并画出折线图来可视化，有时被称做收益拐点。这种设计没有工程应用性质。玩家到达收益拐点需要花费时间、金钱成本，并且很难确保玩家记住拐点前的收益进而对比，我们从上帝视角一厢情愿认为玩家会为此感到高兴、引起兴奋，而未能更“接地气”的从感知有限游戏信息的玩家角度建模。与此相对的是另一种做收益差异的方法，将道具以不同养成模块分组，然后通过组间整体价格放缩做到养成模块之间不同的收益。通常而言，玩家很快接触到这些养成模块，进而迅速的发现收益差距作为付费的决策依据。

比起泛泛而谈的“为体验服务”、“考虑走位和玩家操作水平”、“数值是调出来的”诸如此类的口号而言，可操作性描述了工程实现细节，如同程序员通过编程语言实现功能，数值策划则通过数学工具来得到结果，进而考察结果的充分近似程度，这就是下一节我们要讨论的。

我所接受的工程训练教导我要容许近似，有时候我能够从这些理论中发现惊人的美，即使它是以近似为基础的...我持续在之后的工作中运用这些不完全严谨的工程数学

——保罗·狄拉克

【充分近似】游戏在商业上的成功与许多因素相关，游戏数学建模的好坏作为其中一个因素可以合理的猜想是正相关的，尽管玩家感知游戏里数学计算的表现在敏感度上有待商榷、正相关强度甚至因果强度如何尚未能量化，但是我们仍然要有一些检验解析解可靠性和适用范围的方法，毕竟等待玩家反馈的时间周期太长且已经带来成本损失。自然的，这些方法是仿效工程和物理的：数值模拟与实际游戏。

数值策划出现在大约20年前，早期游戏开发对数学计算的需求并不大，经过粗略计算后程序开发出AI，如果AI在操控单位、种族、阵营对抗时没有明显问题，那么剩下的就留待版本更替解决，这种数值模拟现在仍然是检验解析解的有效方式。然而，随着游戏内容的增加，通常我们不能亲自或等待开发全部游戏功能，所以设置一个理想环境如将战斗的概率表现用期望计算或编写代码模拟战斗是一个可选方案。由于涉及较多的推导、证明，以下仅举一例，更多的例子将出现在【有用的模型】里。

我们有，



该式在说如果单位生命和伤害能力都变化到k倍，则p的变化与k^2有关，记为p(k)。我们用p衡量付费额度或养成模块属性量对玩家的影响，需要知道额外得到的属性与k的关系。存在诸如防御、闪避、暴击、穿透等类生命和类伤害的属性使得k的解析解计算时间复杂度较高，这迫使我们寻找近似解。

已知类生命和类伤害属性只有2种处理：非负实数映射到[0,x]区间（如闪避率取值0%到100%、暴击伤害提高300%）；直接运算（如真实伤害是额外的伤害值不被免伤率抵消）。对于后者，根据具体运算规则，可以视为生命和伤害的线性叠加，对于前者，其取值范围我们不会在不同角色间差距太大，因此我们可以说，



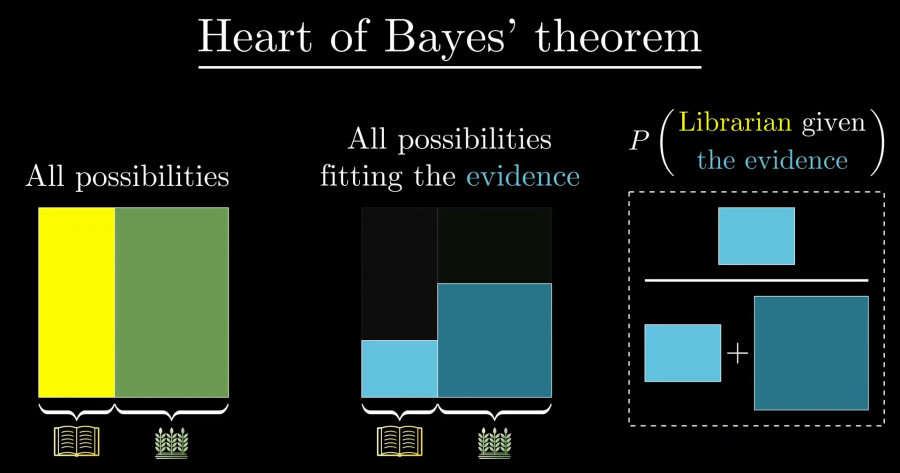
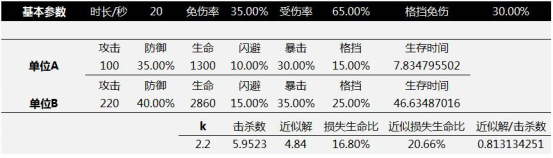
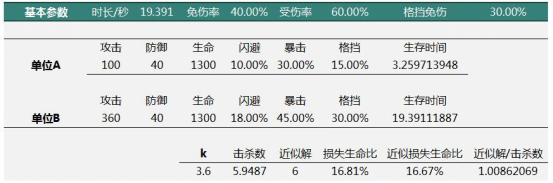
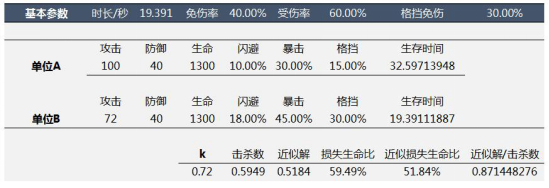
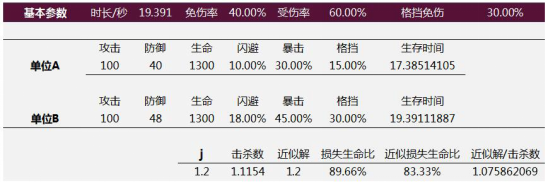
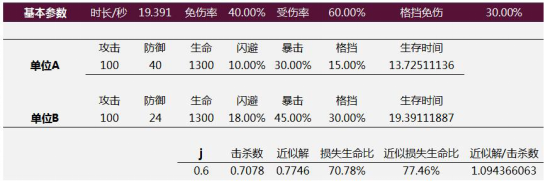
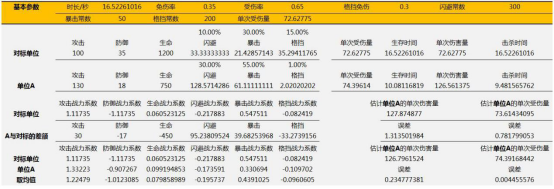
HP(·)是将类生命属性等价为生命值的函数，DPS(·)同理。即全体属性变化到k倍约等于原本的生存和伤害能力变化到k倍，于是p(k)≈1/k^2。这种近似是否足够好呢？如图所示：



解析解得出单位B以16.8%的生命为代价击败单位A，近似解为20.66%，比为81.31%，对用于评估属性变化相比起标的单位有多大的战斗优势，进而得出付费体验和属性量是否合适的判断而言，该精度足以胜任。较低的时间复杂度得出较好的精度，我们称建模是充分近似的。上述例子仅针对乘法伤害公式，因为只有乘法伤害公式才会将防御值映射到[0,1]区间并和攻击方属性无关。

一来，编写代码模拟亦或理想环境计算终究是对现实的简化，二来有些解析解无法列出计算公式检验或编写代码检验需要太多的时间。这就要求在实际游戏里进行工程实验并收集数据来比对算法预期，所谓实际游戏不仅仅像普通玩家那样进行游戏，还需排除其他因素进行工程实验，检验结果是否充分近似。比如存在闪烁、昏迷、放逐等等特殊的技能效果，如何建立这些效果对战斗的函数关系可查阅【技能建模：三种算法的综合】，我们选取已经做好战斗平衡但不同效果的各个角色互相对抗，排除基本属性带来的影响，从而确定技能效果建模的解析解可靠性。

道具的产出与规划将影响玩家的养成情况，养成情况又与战斗强度关联，进而影响PVE里怪物强度的匹配。所以，一个能良好估计玩家战斗强度的建模方法尤为重要，这个方法我们将在【经济建模：齐次方程组与样条插值解】里看到。换言之，实际游戏理应验证估计的玩家强度，存在偏差太远时，应检查养成是否充分，如果充分则检查是否匹配经济的产出和规划。通常来说，玩家强度的估计错误往往是经济规划存在问题，使得玩家不能充分接近规划的游戏节奏，也就无法达到相应的强度。

随意添加、滥用参数和运算法则

在工程应用领域总会存在理论滞后于实际现象和需求，这迫使物理学家和工程师从实验数据里建立经验公式，比如根据探测到的地震波强度估计地震中心地带距离探测点有多远。要说这些经验公式是强行凑出来的不为过，但只要它们是基于数据的、有一定预测价值的，我们就会使用它们直到理论得到足够发展。

然而，一些数值策划在公式上的使用则除了凑出来外，与工程或物理的经验公式出发点毫无相似之处。除法伤害公式，一个生生凑出来的伤害计算方法：



变换为形如“攻击*（1-免伤率）”：



而减法伤害公式为：



免伤率比起减法伤害公式添加了对方防御的反向约束，这加剧了减法伤害公式本有的非线性特征，使得攻击、防御的变化不能有效预测对方的受损情况，或根据目标损血比例逆运算出攻击、防御。解析解的带入具体值当然可以做到，但面对复杂的战斗设计时，解析解的计算相当的繁琐甚至无从下手（如增减属性的技能可施加在任何角色上）。此外，它的防御不够直观，减法伤害公式的玩家知道多少防御就能抵消多少攻击，乘法伤害公式则转换为免伤率展示在界面。除法伤害公式不论在时间复杂度与可预测，还是玩家的易理解上没有任何优势。

除法伤害公式凑出来的思路不得而知，但从滥用运算法则的现象上可一窥一二。这些运算法则的添加可以出现在包括伤害公式的任何公式里，它出现的理由仅仅是希望快速增长便添加多项式、指数或参数间相乘，希望抑制变化时便添加根号和除法，甚至还有使用三角函数来得到周期变化的，仿佛运算法则不是描述现象间关系和推导得来，而是用来获得虚假的操控感，这大大增加了模型的非线性特征。

参数的滥用尤为值得指出，简单的如升级经验公式要用携带多个参数的多项式，而改变这些参数仅仅用来查看公式计算结果是否满足所需。复杂的则有在PVE怪物每个属性上配以用来线性放缩的参数，原因在于实际战斗时常不满足理论预测，调节这些参数更仅有依据属性影响方向来大概逼近需求结果的作用——然后打开游戏再看看情况。设置所谓普通怪、精英怪的参数模板加剧了这点，因为模板是固定的对玩家角色造成伤害，而关卡策划使用多少个这类怪物则有其设计考虑，据此，怪物的数量就大大影响了实际战斗表现，从而进一步依赖对应属性的参数调节，如果其他因素诸如经济建模不够精确，更使得怪物的表现如同云雾一般难以看清。



由于目的、定义和计算上的含糊，战力这个概念被用于许多奇奇怪怪的处理。有一种方式是根据战力计算出属性、平衡，而属性在平衡上的基本指标是“有限的时间t”、“100%生命值”，违反基本指标根本不可能得到正确的结果。当然，将各个属性的战力系数理解为某种投放比例，然后给某个养成模块战力额度，以战力额度的大小来决定养成模块的重要性并期待玩家对此进行判断并非不可取，然而玩家还存在战力能精确表达角色强度的要求，高战力被低战力击败是一件挫败玩家信心和感到不满的事情。此外，玩家互相看到的战力往往是一个总值而不是每个养成模块的战力细节，于是，用战力额度决定养成模块的重要性和引导玩家判断的真正效果就显得可疑了。

还有一种更可疑的使用方法，用售卖价格除以战力，并把这种计算结果叫做性价比。仿佛玩家花钱只是为了让战力数字上涨一般。正如上文所谈论的玩家对战力的实际感知和需求，这种处理方法是真的在面向玩家建模吗？

价值也是一个被滥用的对象，它有时指售卖的价格，有时又代表道具、技能效果、属性强度等之间的大小关系。这使得它甚至出现在和经济无关的地方，比方说技能价值。一些情况下谈论的技能价值是指一个养成模块携带了基本属性和技能，那么这个养成模块的售价会因技能的存在变得不同。另一些情况下却指技能之间的平衡，用价值来衡量技能之间的强度。当它指代售卖价格时，或许其定义和计算还存在不少共通处，但当它指代某种含糊的平衡性时，则干脆不知所云，建模方法也含混不清。



任何一名了解统计回归的人都会对所谓的反推数值感到迷惑不解。排开一厢情愿的目的：复制一款商业成功的游戏数值就能确保数值乃至盈利上的可靠性。在统计学工具上如何实现则停留在excel趋势线拟合上——普通最小二乘法。反推的人并不关心普通最小二乘法的假设和适用情况，自然也不懂得其他的回归分析。这种知识和技术上的匮乏招致了对实实在在困难的低估，采集一款游戏的数值数据所耗费的大量时间甚至金钱，如果他愿意付出代价，还要面临这些问题：假设过强、模型预测、模型扩展。

假设过强是指适用条件太苛刻，现实情况极少满足。普通最小二乘使用简单的多项式拟合数据，这在常规统计和机器学习应用里用于刻画现象是很好的工具，现象背后真实的模型常常是未知的，现象背后的因素也未能全部纳入，我们用方程来尽可能的描述它。然而不同于自然和社会现象，游戏数学建模还没有人能用一个多项式来做全部工作，反推数值仿佛在假设游戏数值在各个模块的建模仅仅是简单的多项式方程得出，无视其本身有着数学建模的原理和过程，不去构建它却去拟合它无异于缘木求鱼。

时间和金钱的有限决定了认同反推数值的人不可能对一款游戏的数值全面测试、采集数据。当他使用有限的数据，却要做总体推断工作来进行模型预测时，excel的趋势线拟合还远不能胜任。在统计与机器学习的应用中，我们使用K折交叉验证来检验模型的外推/泛化能力，这方面的知识足以让人消化相当长时间。此外，模型的解释变量未必对泛化有正面贡献，这就涉及到稀疏估计的变量选择问题。对于一名在统计与机器学习应用上乏可陈列的反推数值者来说，模型在预测未采集的后期数值变化方面和双眼一抹黑相差无几。

复制一款游戏的数值就意味着要几乎全面模仿它的系统规则，这一点对程序开发没有多大困难。但对于广泛存在的或大或小变动的需求以及克服上述反推数值的重重困难后的模型而言，则几乎没有模型扩展能力。要么拿着这摇摇欲坠的模型继续外推，要么主观修改模型参数来分段处理，或者：认真开始建模——那为什么一开始不这么做呢？



不同于高度抽象的纯粹数学，我们使用函数是为了建立、描述和预测现象。然而，很多时候这些现象的函数表达式难以直接得出，但是现象的变化却容易用高阶导数描述，这时，高阶导数与现象存在简洁的关系，而这便是微分方程的建模思路。

技能循环是其反例，一些数值策划“勇敢”的直面繁多的技能，穷举它们，然后纳入一个有限的时间里一字排开，或数值模拟或excel呈现。不论哪种方法他们都在焦头烂额、疲于奔命的实测-调整-实测里浪费大量时间，结果也往往不如人意。相反的，如果我们将技能的伤害、治疗、能量消耗等均用每秒1个常数来描述，那么情况就大大简化了：一阶导是一个常数，与技能表现是线性关系。以伤害技能为例，我们有：



tdps表示随时间累积的伤害量，t为时间（默认单位秒），C表示每秒伤害是一个常数。一个技能的时间表现有施法、冷却、间隔生效，其中普通攻击是技能的特例：



atk是普通攻击的每秒伤害，conjure为施法时间，cd为冷却时间，x为技能的一次伤害量，I(·)为示性函数，满足条件取1否则取0，该示性函数表示如果一个伤害技能的conjure不小于cd，那么玩家无需发动普通攻击，而普通攻击的行为只能发生在cd期间，因此从秒伤角度看它实际秒伤仅为cd/(conjure+cd)的比例。给定其他参数，求出x就是我们的目标。这个式子阐述了一个事实：任何技能的施法和冷却时间不能同时为0。这很容易理解，如果为0，那么C是一个无穷大的量，角色将在玩家操作反应时间内消灭任何敌人。

正如前文所述，模型是对现实的简化和比喻。真正的技能表现并非连续可导函数，而是高度离散的，平均为每秒伤害只是一种近似或平滑处理。更多的讨论我们将在【技能建模：三种算法的综合】展开。









伤害公式是一种函数或运算规则，旨在将生存与输出属性换算成具体的伤害量，一个好的伤害公式应当具有如下性质：

1、线性组合是可逆的。总伤害由不同强度单位的伤害线性组合而成，可以从总伤害逆运算每个单位的伤害进而知道它的攻击力。其中N是第i个怪物的伤害，存在一个系数β满足逆运算得到怪物的攻击力a，可逆性便于根据要求的战斗结果计算出相应属性。。



2、输出型属性与伤害结果是线性关系。这种线性关系可以是与伤害值线性变化，也可以是与伤害结果的一阶导线性变化，如兵力损失的变化量。

本节旨在讨论减法伤害公式的应用（下称减法公式），由于非线性、不破防等性质，减法公式被认为只适用于没有不同武器的不同攻速、BUFF改变攻速这样的简单战斗，或是不便于进行战斗平衡的处理，并且不难发现，减法公式不满足上述“好”的伤害公式的性质。尽管存在这样那样的困难，我们将推导并证明，在一定前提条件下减法公式将具备上述性质，表现得如同乘法伤害公式，由于没有乘法公式的免伤率换算——这会带来对等级压制的设计要求——进一步扩大简单的防御抵消等值攻击的易理解性优势。

第一步是解决这样一个问题：给定任意攻击和防御值，若攻击变化到k倍、防御变化到j倍，伤害量变化到原来的多少？由于伤害量的变化与生存时间是线性相关的，所以解决该问题将直接影响模型的预测和控制力。诚然，带入具体的攻击和防御不难得出解析解，但如果一个改变攻击、防御百分比的BUFF可能施加在任何单位身上，或是给定副本内玩家的总hp损失比求全体怪物的相应属性时（只有乘法公式攻击和伤害的关系满足线性可加性），解析解的实用性是大打折扣甚至无从下手的。数值模拟经验性的表明，在最高免伤率<0.8，初始免伤率<0.45的情况下，攻击变化率与伤害变化率的关系是一个非初等函数：



rdps表示伤害的变化率，k为攻击的变化率，rdam为受伤率，1.5是从数值模拟中得到的经验分界点，在分界点分别使用这2个公式计算是充分近似的（由于不是在制造原子弹，我们可接受的误差最多在20%左右）。我们首先证明第二个公式，它仅需基本的极限知识，其思路为，若k趋于∞，则rdps也趋于∞，两者的比值是否仍然趋于∞呢？



a和b分别表示攻击与防御值，变换为：



因为k趋于∞，所以分母的b可以忽略，于是：



这正是我们需要的。不过，k是在渐近意义上与rdps线性相关，实际中k通常不会特别大，它有实用性吗？幸运的是，数值模拟表明，拜非线性性质所赐，k无需太大就能收敛，而且加入暴击、闪避等属性，该式仍近似的相当不错。



为什么一个仅有攻击和防御的假设环境且渐近线性，仍然很好的近似到真实的存在暴击、闪避等类生命/伤害属性的游戏环境中呢？其实不难理解，因为这些属性生效规则不一样但互相对抗，这使得近似解的误差不会总朝着一个方向发散。

遗憾的是，在极限意义上防御只会令伤害趋于无穷小，这使得生存时间趋于∞，即发散的，我们无法用同样的方式找到防御变化率与rdps的渐近关系。不过，第一个公式将为我们带来有限范围的近似解。考虑：



近似一个函数的方法是模仿它的0,1.....n阶导数，这便是泰勒展开背后的直观几何。不过，如果直接对这个式子里的k求导，它只会告诉我们dps’=k。用k近似效果非常的差，但根据第二个公式推导出的k与rdps存在着与受伤率的关系，我们为什么不尝试工程数学上的粗暴处理呢？舍掉会推出dps’=k的参数，仅保留括号内的受伤率信息，我们有：



对k求导得：



同除b：



显然，1/(a/b)是一个不大的数字，我们忽略掉，于是仅剩1/k^2。左右两边同乘k^2，于是：



即dps变化到k的平方，这正是我们第一个公式已经给出的。数值模拟结果如图所示：



让我们进一步利用免伤率、受伤率在近似解里的价值。



因为b/a是免伤率且为倒数关系，于是防御变化到j倍是：



将防御的变化近似为对方攻击量的变化，然后逼近伤害量，这种二次近似误差只会更大，我们用开方去平抑误差：



接下来我们证明用开方平抑误差的合理性，即我们只需证明误差函数是非线性的增函数。我们首先证明误差不是线性的，由于：



是在k趋于∞时渐近线性的，注意到不等式：



所以在k^2的近似下，误差不可能是线性的，k^2>=k也意味着误差不可能收敛到0，而是发散的，因此不可能是减函数。误差函数不是线性减函数，则只能是非线性的增函数。由于我们不清楚误差函数的表达形式，但对非线性进行根号逆运算会是一个不错的逼近，如图所示，数值模拟表明j在1+0.23内，以及j<1时再度开根运算可近似足够充分：





j不能超过1.23是一个数值模拟经验上界，同时也是理论分析支持的：j如果一直增大，那么免伤率趋于100%，生存时间趋于∞。∞是发散的，我们无法近似一直在变大的数。

有了上述近似求解方法，我们可以得出减法公式下的战斗平衡和战斗优势的估计。若一个单位的整体属性提高m倍，那么：



将m移到分母位置：



于是：


我们查看数值模拟：



近似效果一般，超出我们容忍的20%左右误差。不过，继续数值模拟会发现近似解几乎都在低估，所以，近似解可以作为下界，提高了m倍的单位至少能够对抗的数量或至多损失的生命比例。在通常用来评估强度差异时，已经够用了。

攻击速度指间隔t秒攻击1次，取倒数变成每秒攻击n次称为攻击频次。显然，攻击1次是1倍伤害，攻击2次是2倍伤害，以此类推我们知道攻击速度想要保持平衡，只需减法公式运算后面乘以相应攻速即可保证。然而根据这样的理解，这不能适用在不同攻速的武器上，否则玩家会看到相同的攻击值但不同攻速，这会给玩家带来困惑。

我们知道，攻击值是各个养成模块的加和：



s是养成模块的数量。加入攻速，我们有：



speedatk表示攻速，b为防御值，dam为伤害量。我们已知k和rdps的关系是渐近线性的，那么speedatk可以表示rdps提高到了等值倍数，求k是多少：



于是：



我们仅需武器模块依不同攻速保持平衡并面板展示攻击值给玩家，其他养成模块在代码中仍乘以武器攻速（因为其他养成模块不会随着携带不同武器而改变自己提供的攻击值）。如果atk_1是武器模块，乘法分配律告诉我们：



已知rpds求k，数值模拟的经验分界点是2：



即，一个武器的攻速小于2时，用武器攻击乘攻速的开方，否则乘攻速和受伤率即可。实际中，speedatk在2的附近进行开方可能大于speedatk*ram，这是经验公式的问题所在，可以自行根据具体攻速决定取哪个来保证攻速大的攻击值也大，也可给予攻速大的在时间劣势上的额外攻击值奖励。



在战斗建模里，一个单位的强度是在它的敌人面前能生存多久、造成敌人多少比例的生命损失。不过，玩家面对众多的属性是不能直观理解到单位强度的，此外，有一个明确的数字甚至进度看到在确确实实的成长是游戏设计在奖励反馈感上的基本法则。战斗力（下称战力）概念就在这种背景下诞生，一个好的战力估计应当有如下性质：

1、线性的，便于玩家理解。
2、充分近似的，战力能够表达单位的真实强度。

基于这2个性质，有一些战力计算方式是不可取的。一种简单粗暴，直接将每个属性的战力系数当做这个属性的单价或单价的中间系数。一种是打分数，给标准模板的每类属性打分，用分数除以属性值得出单个属性的分值作为战力系数，这相当于将战力理解为玩家成长得有多标准。

目前已知的上述两种方式或其他方式，均不具备第2点的性质要求，易出现战力绝对差额大的，战斗结果却是颠倒的，尤其是胜利方还剩余大量生命值，这大大增加了玩家对单位强度如何的迷惑感。本节提出的方法将同时满足这2个性质：

1、推导并证明，对伤害运算里的各个属性求偏导组成全微分加和，将偏导值作为战力系数，充分近似是一阶精度的。

2、推导并证明，在容易满足的前提条件下可以将精度提升至近似二阶、三阶甚至更高阶精度并仍然是线性的。

3、不在伤害运算里的属性战力系数估计，如回合制的速度。

已知伤害运算F(a0,a1,...an)是一个多元函数，其中a表示具体属性，在k处进行泰勒展开至一阶，有：



f(1)(·)是F(·)对a的一阶偏导表达式，h表示a和ak的差额，也叫步长，O(h)表示截断误差与步长有关。所谓k处，指我们选择哪个单位/职业/角色作为攻击方和被攻击方，称对标单位，它的具体属性值就是k处，代入具体值很容易算出f(1)，从而得到各个属性的偏导值作为战力系数，并将这些战力系数同等的应用在其他单位/职业/角色身上，而其他单位的每个属性值与对标单位之间存在差额，差额即步长，由于截断误差与步长有关，并且我们只取了一阶线性项，显然其精度是一阶的。

线性性质已经满足，充分近似是一阶精度的，但除非步长充分小，否则我们的误差以二次方的速度累积。在实际中存在着多个兵种、职业，无可避免的一些兵种、职业的各个属性与对标单位的属性差额很大，那么保持线性来改进一阶导的值，进而提高精度就被自然引出了。

我们将多个兵种、职业视为多个可展开点k1,k2....kn，n表示兵种/职业数，k1是对标单位。如果我们选取k2也作为展开点，一阶展开为：



又有k1的展开点，其偏导表达式为：



而k2的偏导表达式为：



将两者取均值，则：



如果我们将k2处的偏导视为是在k1处的展开，则有：



将其中的一阶项代入取均值的式子中：




合并同类项：



而F的二阶泰勒展开是：



显然，我们在避免二阶导的非线性处理下，通过加入另一个兵种/职业的一阶导和对标单位的一阶导取均值提高了精度，忽略混合偏导数项，则截断误差介于二阶和三阶，精度在一阶和二阶之间。比较精确解与估计间的误差，如图所示：



估计伤害的误差从1.313下降到了0.234，受伤的误差从0.781下降到了0.004。

既然考虑进新的单位可以将精度提高到近似二阶，那么再加一个单位是否能提高到近似三阶呢？仿照龙格库塔法，如果：



λ表示F在ki处偏导数的权重，即多个单位作为展开点处的一阶导，通过加权平均得到一个更好的一阶导。这个λ有无穷多解，所以一般而言取值为：



其中k2单位生存和击杀时间必须介于k1和k3之间。精度改善如图所示：



误差列从上到下分别是三阶、二阶、一阶估计后与精确解的误差，三阶的误差是最小的。然而我们还能看到二阶估计反而不如一阶估计，其根本原因在于，我们的精度并不是严格二阶、三阶乃至更高阶的。因为一个多元函数的泰勒展开还包含混合偏导项，我们却使用应用在一元函数上的泰勒方法分析，忽略混合偏导，使得误差并不总能缩小，根据多元泰勒展开的混合偏导表达式，可以知晓忽略带来的误差随着步长呈指数级增长，指数等于选取的单位数。这提示我们，除非对标单位与其他所有单位间的属性差额（步长）尽可能的小，否则误差会很轻易的增大。显然的，中位数是离其他所有数据点差额最小的值，如果我们将所有单位的生存与击杀时间排序，时间在中位数位置的就是最佳对标单位，中位数附近的是最佳高阶展开点。比起当下常见做法，随意选取一个对标单位，如稻草人。泰勒展开的分析告诉我们，应当选取距离其他所有单位差额最小的。

接下来我们讨论不在伤害函数里的属性，甚至没有伤害概念的如女性向对拼衣着打扮的属性如何估计其相应系数。事实上，这可以转化为一个最小二乘问题。以回合制常见的速度值决定出手顺序为例，每个单位都有不同的速度值，若速度值s满足不等式：



那么，出手顺序满足：



即不论计算函数如何，速度值大的就是出手靠前的，或将速度槽最快累积满的。我们假设出手速度会影响单位的强度表现，那么我们在求如下优化问题：



θ是我们需要估计的每1点速度值增加的战力，tdps为累积伤害量，指在对标单位面前生存回合内总伤害值，b为截距，s为速度值，n为单位数。公式是最小二乘的优化目标函数，求出使得式子达到最小值的θ，这一点，excel趋势线便能解决，如图所示：



得出速度的战力系数约为27，这是个令人惊讶的数字，完全与在伤害函数中的属性战力系数差距很远。这个问题在于，不同单位的速度值、伤害量之间的量级可大可小，甚至不同游戏之间也是如此，数字大的被认为影响更大，但实际单位之间强度并非如此。比方说，A比B强2倍，A的输出为100点伤害，B为50，在另外的数学建模中A的输出为20000，则B是10000，然而A保持是B的2倍强度，因此，我们需要回归分析里的一个数学处理方法——标准化。将速度值和累积伤害都标准化到均值为0，方差为1的正态分布下。标准化公式为：



速度值减去其均值然后除以其标准差，累积伤害同理，标准化后估计出的系数如图所示。



每1点速度提供的战力系数为0.418，这便显得合理多了。

标准化后的最小二乘估计还能应用在没有伤害概念的游戏里。比方说一些女性向游戏只通过衣服品质来比对高低，如果搭配品质不一则根据其具体的魅力、时尚之类的属性值判断。可以将衣服品质赋予数值，然后进行最小二乘估计。



在所有战斗相关的建模中，我们面对的最复杂的情形之一便是技能。技能的设计充满了想象力，这对数学计算发起了挑战，以当前游戏数学建模

参与评论